It has been generally demonstrated that, because human brains are wired toward pattern detection, we are lousy at intuitively interpreting statistics; this is the main reason why casinos are viable businesses. Trying to do anything to curb this problem often results in the worship of the Random Number God, or beliefs like:
- The hit/miss belief: "A hit ratio below 25% is hopeless and a hit ratio above 75% is guaranteed. Everything else is a crapshoot." This stems from our evolved propensity and preference for quick decisions, so we often round everything up or down, in this case to 100%, 50%, and 0%. Obviously 75% does not equal 100% nor does 25% equal 0%, but you'd be surprised how often people forget those were just crude approximations.
- The Gambler's fallacy: All probabilities should somehow "even out" while you're playing, or the belief that a random sequence of events has a "memory". For example, if the computer has a hit chance of 50%, and hits, that's okay. However, if it then scores another hit right away, The Computer Is a Cheating Bastard. In truth, it just happened to be the way the "dice" fell. As is often stated, "dice have no memory." In situations where extreme good/bad luck streaks are undesirable, the Gambler fallacy can be invoked, chiefly in the form of pseudo-random distribution (or PRD). Under PRD, consistent misses will slowly increase the chance of a hit, and vice versa. Many video games uses this variant of "random" without being noticed, because "pseudo-random" feels more random than real random. Note that there's a nugget of truth in the idea that odds should even out eventually, the operative word here being eventually; this is known as the Law of Large Numbers.
- Naïve Combination of Probabilities: Given the probabilities of two events, people will often simply either add them or multiply them. Generally speaking, calculating the combined probability is much more complicated. For example, suppose you roll a die twice. The probability of a six is 1/6 each time, so the probability of at least one six in two rolls must be 1/3, right?note
- The Definition of Probability: There are two ways probability can be defined. The first is what should happen in a random process in the long run. The second is the degree of certainty with which a belief is held. The first definition applies to statements like, "The probability of rolling a six on a fair die is one in six." The second applies to statements like, "My favorite team will win this game." This difference can be very important. These two views are called frequentist and Bayesian, respectively.
- Decision-Making and Probability: When a reasonable decision was made according to the odds, where the odds are calculatable, a measured risk is always taken. If this somehow backfired, calling this a wrong decision is fallacious because that would imply clairvoyance is presumed; conversely, when all data and signs are ignored, thus a silly decision was made. Even if that worked out in the end that doesn't make the decision any less ill, as that's just literal dumb luck. For example, if two gamblers agree to roll a fair die, betting 1:1 where Gambler A wins on a 1, and Gambler B wins on a everything else, Gambler A is making an irrational decision to bet — the outcome of the dice roll has no bearing on said irrationality. If it's stupid and it works, it's still stupid and you're lucky
- Even Probability Distribution Fallacy: When someone assigns equal probabilities to a list of possible events where an even probability distribution cannot be presumed: "The suspect either shot the victim or he didn't shoot the victim, therefore there's a 50% chance he shot him." Ad Absurdum, one would have to claim that you have a 50% chance of winning the national lottery because you either win it or you don't. 50% is not a bad guess when you have nothing else to go on, but only if you have nothing else to go on.
- Projecting From a Small Sample Size: Even a fair coin has a significant probability of coming up heads seven times in ten flipsnote , so you can't project from such a trial that the coin has a 70% probability of coming up heads. Although there is no real "minimum sample size" to speak of, most accept the arbitrary magic number of anywhere between 20-50 (most notably 30). Obviously a higher sample size will grant better results, even though it might not be cost effective. In academia this isn't a problem as long as the sample size is shown, so the readers can decide for themselves whether the sample size is good enough. But your everyday layman will not notice this detail, and thus are prone to erroneous conclusion from scientific statistical research.
Note that while this often makes fun of the developers messing up at statistics or the author having no clue how it works, this can actually be invoked or justified.
Compare Lies, Damned Lies, and Statistics, when statistics are not just used incorrectly, but are manipulated to get certain results.
Also see 20% More Awesome, which involves quantifying the unquantifiable.
Examples of how this plays out in storytelling:
- It's common for a naïve poker player to (correctly) fold a bad hand, such as flush draw with no other outs, to a large bet, only to lament their "mistake" when it turns out their hand would've improved on the turn or river. Especially naïve players may try to "correct" their mistake by calling the next time they find themselves in a similar situation, which more savvy players can exploit.
- In Monopoly, you may decide to build houses when you see your opponent will land on your monopoly a throw of 6, 7, or 9 on two six-sided dice.note Anyone with half a clue as to how the game works and basic probability theory realizes that's about as lethal a situation as your opponent could be in (for a single monopoly), and would build. Yet if your opponent throws a 12, and bypasses your entire trap, your decision was just as reasonable as before. It just didn't pan out.
- Many Bridge players feel that the computer-generated hands used for many duplicate games are more unusual (i.e. favor more unlikely distribution of cards) than human-shuffled hands. They're right, but in a backwards way: The computer-generated hands are more likely to be completely random than hands dealt from a human-shuffled deck. Even the best human-shuffled deck will retain a few cards in the same relative order as they were played in the last hand; computer-generated hands don't (except at the frequency you'd expect from random chance).
- German card game Skat has rules in place, that if one player in a tournament has to use a shuffling machine (e.g. due to a disability), everybody has to, because hand shuffled decks are less random and favor the player after the dealer compared to the better randomization of a machine.
- Many players of the online version of Magic: The Gathering are convinced that the algorithm used to shuffle players' decks is flawed and biased. Some say the bias is towards "mana flood", where you get too many mana-producing cards (and not enough spells to actually use that mana with), while others say towards "mana screw", which is the exact opposite — not getting enough. In reality, the algorithm is completely incapable of either, since it does not consider what type any given card is when performing the shuffle. The reason for the dissonance between physical and online play (when there is one at all — mana screw and mana flood are common on cardboard too) is that having to physically shuffle a deck enough to provide a truly random distribution every time would be incredibly annoying, particularly given the number of times some decks end up being shuffled in a single game. Most people just take their land cards, which end up all in one pile at the end of a game and put them into the deck at fairly even intervals to avoid there being giant clumps of nothing but land. For practical reasons, even in tournaments it's accepted that the deck doesn't have to be truly randomly distributed — it just needs to be random enough that a player can't predict what comes next.
- Go to any online poker forum and look in the General Discussion forum. More often than not, you'll find a sticky about the game not being rigged, and an explanation of why it may seem that it is. Most forums will also have a 'Bad Beats' section for whining about the 'rigged' play screwing the loser.
- One popular roulette strategy (called Martingale
 ) is believed to always net you money. The same strategy works the same on any 50% chance double money back bets (or as long as the chance to win is balanced against the payout). The basics of the strategy is to bet 1 on red/black, odd/even, or high/low when you start and if you win, and double the bet if you lose.note The belief is that you will eventually win, and thus win the initial bet.
) is believed to always net you money. The same strategy works the same on any 50% chance double money back bets (or as long as the chance to win is balanced against the payout). The basics of the strategy is to bet 1 on red/black, odd/even, or high/low when you start and if you win, and double the bet if you lose.note The belief is that you will eventually win, and thus win the initial bet.
There are a few reasons why this doesn't work:- To be guaranteed a win, you'd need an infinite amount of money and time. If you had infinite money, you wouldn't need to bet.
- Real casinos always have betting limits, which remove the option to double up at some point. This will generally completely wipe out your winnings thus far that session if it happens.
- If your original lost bet is one dollar and you follow this stratagem, an unlucky streak of ten consecutive losses (including the first) has you betting $1022 to chase after your original loss of a single dollar. Even if you do win, all you get is your original dollar back. You were better off just betting one dollar at a time and hoping for a winning streak.
- The presence of 0 and 00 on the Roulette Wheel, which is a loss regardless of which of the above options you bet on, means that there's not a 50% chance of winning. The odds are actually closer to 47%. With the exception of the quint bet, all of the bets on the table have the same expected outcome, trading win amount for likeliness.
- There is an optional "Event Deck" for the board game Settlers of Catan, which is just 36 cards: one for each combination of two six-sided dice. Using it instead of the dice makes probabilities "even out" somewhat, guaranteeing that in each shuffle each number will come up exactly as often as it "should". To a naïve player, it may seem like the change would be insignificant to the gameplay, but consider what the dice actually do in Catan. Each of the board's tiles (except the desert) is assigned a number which is a dice result; whenever the dice hit it, that tile produces resources for the players who have claimed it, regardless of who rolled the dice. So with the cards used instead, every player knows exactly how much each tile will produce every 36 turns, rather than only a probable amount. In essence, half of the game's random element has been removed (trading which numbers will come up for just when), making it much more a game of just doing the math (and Batman Gambits). Of course, if you try to play this way, but your math skills aren't that fast, you can get Paralysis by Analysis. The deck also opens the game to gaining an advantage by card counting, making it far easier than it would be with blackjack even if a single deck were used.
- In the Asterix album The Soothsayer, the Roman army has been ordered to round up all soothsayers. When soothsayer Prolix claims to be just a fake (which is true), a centurion tests him by making him predict a roll of two dice. Prolix guesses correctly ("7") but then argues that if he was a real soothsayer, he would never have bet on the number that would get him arrested. "7" is actually the most likely result (1/6), but even so, predicting one roll of the dice proves nothing.
- One scene in The Parent Trap (1998) features Annie and Hallie facing off in a poker game, which Hallie ultimately wins by drawing a royal flush as her final hand—which is evidently meant to establish her as a skilled poker player. But drawing a royal flush at any point in a game of poker (let alone as the final hand) isn't just evidence of being a decent player—it's a once in a lifetime occurrence. In most variants of poker, a player's odds of drawing a royal flush are less than one in half a million.
- Discworld:
- The Science of Discworld books have an arguably accurate but somewhat twisted take on statistics: the chances of anything at all happening are so remote that it doesn't make sense to be surprised at specific unlikely things.
Every pattern of raindrops on the pavement is unique. We're not saying that if one such patterns happens to spell your name, this is not to be wondered at, but if your name had been written on the pavement in Beijing during the Ming dynasty, at midnight, nobody would have noticed. We should not look at past history when assessing significance: we should look at all the other things that might have happened instead.
- The books in general contains some variant of "A million to one chance comes up nine out of ten times" that comes up a few times. Of course, this being the Discworld, it actually works. Note that, thanks to the properties of narrativium, it has to be exactly a million to one to work. 836,715-to-one are not the kind of odds you'd ever want to rely on despite them being almost 20% better than a million to one statistically.
- The Science of Discworld books have an arguably accurate but somewhat twisted take on statistics: the chances of anything at all happening are so remote that it doesn't make sense to be surprised at specific unlikely things.
- Dave Barry once joked that he always flew on the airline with the most recent crash, on the assumption that it wouldn't be "due" for another one.note
- Mark Twain's Life on the Mississippi contained the following proof of what you can do with statistics:
In the space of one hundred and seventy-six years the Lower Mississippi has shortened itself two hundred and forty-two miles. That is an average of a trifle over one mile and a third per year. Therefore, any calm person, who is not blind or idiotic, can see that in the Old Oolitic Silurian Period, just a million years ago next November, the Lower Mississippi River was upwards of one million three hundred thousand miles long, and stuck out over the Gulf of Mexico like a fishing-rod. And by the same token any person can see that seven hundred and forty-two years from now the Lower Mississippi will be only a mile and three-quarters long, and Caironote and New Orleans will have joined their streets together, and be plodding comfortably along under a single mayor and a mutual board of aldermen. There is something fascinating about science. One gets such wholesale returns of conjecture out of such a trifling investment of fact.
- The shortening of the Lower Mississippi he is talking bout is the actual length of the watercourse. It is continually being shortened or lengthened over time by changes in its path, for instance a wet spring or summer may cause an oxbow to be cut through, shortening the river, while in a dry year, a bend or curve may be increased, lengthening it.
- In Lois Duncan's A Gift of Magic, the psychic protagonist, Nancy, is given a standard test to detect telepathic abilities. She is asked to pick, without looking, all the white cards out of a deck of cards filled with an equal amount of black and white cards. Because she wishes to hide her ability, she picks all the black cards so that she would get all the "wrong" answers and fail the test. The examiner sees right through Nancy's ploy because there is an equal probability of picking only white or only black cards and explains that if she really wanted to screw up the test, she should have picked a roughly equal amount of black and white cards at random. For reference, the probability of drawing 26 cards of the same color from a full deck would be 1 in 67,108,864.
- The Moon Is a Harsh Mistress: The supercomputer Mike calculates the odds of a plan's success as a whole. At the successful completion of each of the early steps of the plan, Manny asks him for an update on their odds from that point, and Mike keeps giving odds lower than they were before, saying that the later steps in the plan have more opportunities to go wrong. However, these late opportunities for failure (which he was always aware of) should have been factored into every single odds calculation from the beginning. Each successful step should only improve the plan's chance of success from that point.
- Brian Aldiss wrote several stories where humans are near extinction, and where society thus makes heavy use of robots; one characteristic of such robots is that their logic often leads them to mistake clear reasoning for correct reasoning. One such story has this exchange:
"There is more country than city."
"Therefore there is more danger in the country." - Discussed, subverted, and justified in The Wheel of Time book Towers of Midnight, when Noal Charin points out to Mat Cauthon that rolling dice to determine which direction to go won't work, due to the higher likeliness of rolling odds than evens, and Mat counters that his magic luck means that it wouldn't be random, regardless.
- Just before Princess Diana gave birth to Prince Harry, one British newspaper article claimed that if the unborn child was a boy, that would complete a sequence with a "1 in 60,000" probability, and therefore it was overwhelmingly likely that the child would be a girl. This ignored the fact that a sequence of 15 boys followed by a girl has exactly the same before-the-fact likelihood of 1 in 65,536 as a sequence of 16 boys (or of any other specific sequence of 16 births), and that this is because the likelihood of any given baby being a boy is about 50%, regardless of previous births (especially if not births by the same mother, as in this case).
- One book on recreational mathematics described "the college bet", so-called because its inventor supposedly made enough money from it to put his son through college. If you select three card ranks randomly, and then draw a card from a fair 52-card deck, the chance that it will be one of your ranks is 3 in 13, right? Thus (the book claimed) if you draw three cards, the chance of at least one being one of your ranks is 9/13 (0.6923), and with four cards this rises to 12/13 (0.9231). If the author of the book had followed this "logic" a bit further, he would have seen that this gives the chance of one in five cards being one of yours as 15/13, or more than certain — which is clearly nonsense. (In truth, if the cards are drawn with replacement, the three-card probability is 47/85 (0.5529 — substantially worse than the naïve calculation), the four-card probability is 2759/4165 (0.6624), and the five-card probability is 6221/8330 (0.7468); if the draws are without replacement the probabilities are 0.5448, 0.6499 and 0.7307 respectively.)
- A high school science teacher on The Daily Show thought there was a 50/50 chance
 of the LHC creating a black hole and causing The End of the World as We Know It. His rationale? It could happen, or it couldn't happen, therefore there was a 1 in 2 chance of the apocalypse. Artistic License – Nuclear Physics is also involved. Correspondent John Oliver, who was conducting the interview, then suggested that he and the teacher try to breed after the end. The teacher replied that this was impossible, as both were male, but Oliver insisted it would either happen or not happen, a one-in-two chance!
of the LHC creating a black hole and causing The End of the World as We Know It. His rationale? It could happen, or it couldn't happen, therefore there was a 1 in 2 chance of the apocalypse. Artistic License – Nuclear Physics is also involved. Correspondent John Oliver, who was conducting the interview, then suggested that he and the teacher try to breed after the end. The teacher replied that this was impossible, as both were male, but Oliver insisted it would either happen or not happen, a one-in-two chance!
- In the Corner Gas episode "Security Cam", Karen figures that there's a 50% chance of a riot breaking out in downtown Dog River, using exactly the same reasoning.
- On The O'Reilly Factor, Bill O'Reilly argued that life expectancy was lower in the US than in Canada because the US has ten times as many people, and therefore has ten times the number of accidents.
- A common mention on the show Hell's Kitchen, as well as a number of other reality shows, is that at any given time a given contestant has a 1 in X chance of winning the grand prize, where X is the number of remaining contestants. Not only does this suggest that the winner is chosen at random (which is not the intent of the statement), but also that every contestant is equally likely to win. This is untrue, especially on shows which have a number of obvious dud contestants (such as Hell's Kitchen).
- In the Law & Order episode "Coma", McCoy tries to ease Kincaid's conscience about subjecting a comatose victim to a high-risk surgery in order to remove a possibly trial-winning bullet. Subverted in that he's perfectly aware that it's bad statistics.
McCoy: Well, I see one of three things happening: she gets better, she gets worse, she stays the same, and we get strong evidence. Two out of three ain't bad.
- Invoked in Survivor: As the players in the game dwindle, Probst tells them that they have a "one in x shot at winning the million dollars." The way he mentions this, it sounds like the winner of challenges (and at the game period) is chosen at random, when it actually isn't. You can argue that if you're in the final six with The Load and someone who the jury hates, you would have a one in four shot since the jurors would not vote for them. Justified in that he does this to motivate the players and it's part of his "character."
- The mainstream media's fondness for flashy graphics to engage the viewer's attention occasionally lends itself to a few mistakes. Such as a pie chart where the total breakdowns add up to 193%
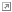 ◊, or this poll with a breakdown that adds up to 120%
◊, or this poll with a breakdown that adds up to 120% ◊. Either with the pressure of the rush to get on-screen information ready by showtime, those responsible have little time to double-check their work; or they care more about making a quick impression on the viewer than ensuring accurate information.note
◊. Either with the pressure of the rush to get on-screen information ready by showtime, those responsible have little time to double-check their work; or they care more about making a quick impression on the viewer than ensuring accurate information.note
- In the "Captain Jerk" episode of Henry Danger they set up a contest where people have to guess a random number to meet Captain Man and Kid Danger. The random number is four digits, but it takes a very long time (a few days) for the final winner to guess the number, especially as they show the entire city obsessively trying to guess the correct number.
- The MythBusters have tackled several things that touched on statistical misconceptions, but probably their most direct assault on this trope was the "Monty Hall problem
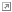 ". In a nutshell, this is when you choose one of three doors that may hold a prize. The host (who knows the truth) opens a different door, showing no prize, and asks you to keep your original choice or choose the remaining door. The hasty assumption is that this second choice is 50-50, and people will tend to stay with their first door, but the reality is that changing your choice has twice the probability of success. The MythBusters demonstrated that much experimentally, with one hundred trials (fifty each way). When they tested the other half of the myth, the psychology of it, twenty out of twenty of their test subjects stayed with their original choice, many claiming that it was because of the supposed 50% chance.
". In a nutshell, this is when you choose one of three doors that may hold a prize. The host (who knows the truth) opens a different door, showing no prize, and asks you to keep your original choice or choose the remaining door. The hasty assumption is that this second choice is 50-50, and people will tend to stay with their first door, but the reality is that changing your choice has twice the probability of success. The MythBusters demonstrated that much experimentally, with one hundred trials (fifty each way). When they tested the other half of the myth, the psychology of it, twenty out of twenty of their test subjects stayed with their original choice, many claiming that it was because of the supposed 50% chance.
- In the Only Fools and Horses episode "A Losing Streak", Boycie refused to bet on a coin toss against Del because, having beaten Del in the previous few tosses, the "Laws of averages" dictated that he would likely lose this one. When Del suggested that Boycie challenged Rodney instead, he agreed!
- Drexells Class has one of Drexell's students reveal that he's skilled at counting cards. He demonstrates by correctly identifying the top card on the deck and then does so again with the next card. This isn't how counting cards works. The kid would only know which cards are remaining in the deck, not their exact sequence.
- Community: While running a psychology experiment Prof. Duncan has a total breakdown when he encounters the outlier of extreme patience that is Abed, ranting that his Duncan's Principle has been completely broken. Of course any scientist can tell you a single outlier is hardly enough to totally disprove a hypothesis concerning human psychology. Possibly an intentional example, since Duncan is clearly demonstrated throughout the series to be a fairly inept psychologist.
- One Scrubs episode began with JD giving the (presumably correct) statistic that, if you discount the maternity ward and the emergency room, one out of every three people who go into a hospital will not come out. The episode then focuses on JD, Turk, and Elliot, each of whom is tending to a new patient, with the obvious implication that one of the three patients will die. The result? All three of the patients die. Dr. Cox, in the ending, points out to a depressed JD that statistics are only useful in the aggregate, and can only tell you what is likely to happen in an individual case.
- Dave Gorman's Important Astrology Experiment,in which Gorman lived his life according to his horoscope, and kept track of how well he was doing on three scales: Health, Love and Money. The first two were on scales from -100 to +100, the third was just in pounds. So already having (or being in debt for) more than £200 swamps the other two altogether. Even worse, when he had a positive score on his arbitary cut-off point (because he'd won a longshot bet) he treated that as the "final result", rather than looking at the trends (which were ... not good).
- Wrestling commentators discussing multi-person matches frequently claim that the champion in a 4-way match only has a 25% chance of retaining his title, with no regard to comparative skill levels or possible alliances between the participants. Given the fact that the outcomes are always predetermined, however, neither skill nor chance really has anything to do with it.
- Cox and Box: In the (sometimes cut) gambling number, the titular characters roll nothing but sixes on their dice, leading them to suspect the other is cheating. Although they both are, no dice-weighting is quite that good.
- Deconstructed in Rosencrantz and Guildenstern Are Dead. A coin flipped 85 times comes up head each time, and they try to figure out how it's happening. Two explanations Guildenstern develops are divine intervention and random chance. The ultimate reason is that they're characters in a play, so the author is making it happen.
- F.A.T.A.L. says that to determine the probability of an event, you roll two percentile dicenote , and if the second one is equal to or greater than the first, you succeed. That means that everything has a flat 50.5% chance of happening. And yes, you're supposed to do this for anything that doesn't have a specific rule for it.
- Warhammer 40,000: Fears of "bad dice" abound. The previously mentioned lack of even distribution and the tendency of rolling methods to influence the result only adds fuel to the fire. Bad dice can be a real thing. Las Vegas maintains a very strict policy for evaluating the balance of dice BEFORE they go into a game, and replacing them at regular intervals. As most 40k players play with cheaper, mass-produced dice, and will rarely replace them unless they have visually obvious defects, it is perfectly plausible for a player to be using biased dice.
- Blood Bowl: There's almost always at least a 1 in 6 chance of succeeding or failing because when rolling a d6 (i.e. most dice rolls), ones always fail and sixes always succeed. Players hate this because you tend to fail at the worst possible time. Failing also ends your turn in most cases, so superstition abounds.
- In the A Song of Ice and Fire roleplaying system, there is a table for rolling random events in your family's history. This would be perfectly fine, except that you roll three dice for the events (thus making the events in the middle more likely) and the table is in ALPHABETICAL ORDER. Thus, Doom (the worst thing that can possibly happen to a family) is more likely than a mere Catastrophe (still bad, but not even half as bad), just because Doom is closer to the middle of the list than Catastrophe is. The results are very true to the setting.
- Dungeons & Dragons players often work under the rule of thumb that a character's intelligence (INT) is equal to IQ/10. While this works well enough for the most part (the average human int is 10 and the average human IQ is 100, where as the highest IQ a real person can have seems to be around 210, and 20-21 is about the highest INT a human can have without magic or the like), the whole deal is a pretty big oversimplification as, to name just one problem, there's more than one kind of IQ test while the INT score assumes there is some objective, universally agreed upon way to measure intelligence.)
- MMO players, almost without fail, will adhere to mindset two — they will notice the streak of resists/misses/landed enemy attacks/what have you that killed or almost killed them, but never notice the long, long, long string of hits that precede it. Any and all MMO forums will have a topic pop up fairly regularly asking whether (or sometimes screaming loudly even with no evidence to that effect other than they had a string of bad luck) the RNG is broken.
- ...which can lead to no small confusion at times.
- This kind of fallacious reasoning reached memetic proportions in the pre-expansion World of Warcraft encounter "Onyxia's Lair." A player who'd run into a string of bad luck assumed that the developers had made the encounter harder, and loudly complained: "She deep breaths more!" (Not breathes, breaths,note ) Today, "She deep breaths more" is the official name of an in-game achievement you can earn in Onyxia's Lair.
- To further complicate things, some MMOs actually do use a skewed RNG, precisely because true randomness could, in theory, result in a string of misses one real day long, or the opposite. Since MMOs rely on a very predictable form of randomness (e.g., no plucky level 1 can be able to beat a level 20 monster because the monster miraculously rolls no hits, but if attacking a level 4 he must be able to win through pure luck some of the time), various measures can be put in place to make sure the game generates the good, reliable sort of random.
- The biggest place this tends to show up is in loot drops, in order to ensure that a player gets loot AT LEAST so often. This is actually very important for helping to maintain addiction.
- Because of players complaining about this, the drop rate formula for quest items was changed to increase the drop percentage every time the quest item required doesn't drop and reset it after one does drop. This is also to avoid the wild variation in time a quest can take when it's truly random. The formula for non-quest-related gear drops, however, is still truly random and doesn't vary from one attempt to the next.
- The players' failure to get how probability works was joked about in the 2015 April Fool's Day patch notes, which presented a large number of fictional changes to the game, one of which was:
The S.E.L.F.I.E. camera mission "Field Photography" is not appearing for all players due to its random nature. We didn't change anything; we just wanted to point out what random means. - Fire Emblem:
- All games after the fifth display inaccurate hit/miss percentages.
- In most cases, the game actually uses the average of two random numbers to determine a hit, so a 75% chance to hit is really 87.5%, while a 25% is actually a 12.75%. This system is likely in place to make dodging-type units evade more (and thus more viable) and high-accuracy characters strike more and lessens the chance that such a character dies (Due to permanent death and limited saving, this means restarting the entire level in most games) against all 3 of the random mooks that has a 2% chance to hit each. This system does tend to benefit the player, as their high powered heroes almost always have greater than 50% odds to hit, meaning the system results in them hitting more often than the displayed percent, while enemy mooks are much more likely to be in the sub-50% range, making them miss more often than they otherwise would.
- From Fire Emblem Fates onward, a different RNG system was put into play (it vanished in Fire Emblem: Three Houses, but returned for Fire Emblem Engage). How it works is somewhat complicated, but in brief, it follows a similar curve to the one above if the hit rate is above 50% (albeit slightly reduced), but if the hit rate is below 50%, then the hit rate is calculated normally as a simple percentage roll. This means that characters with lower hit chances, mainly enemies, are considerably more of a threat, making "dodge-tanking" less reliable.
- A major note of irony to all this is that fans will often claim the RNG in older games or post-Fates games is "cheating", when it's entirely fair in the former case and at least far closer to reality in the latter case. A character missing two 80% hits and then getting hit by a 20% hit sounds unreasonable at first, but in a fair system, that's only a 1/125 chance of happening: unlikely, sure, but when there are dozens of rounds of combat every chapter, it's almost guaranteed to happen at some point. Meanwhile, in the case of the "2RN" system, that chance declines to around 1/1800.
- To prevent Save Scumming abuse, the tenth game's (unlike the ninth's, which was completely random) bonus experience system note always increases exactly three non-capped stats (unless of course there aren't three to increase), selecting which three with a roll weighted by their relative growth rates. This just wound up making bonus EXP differently exploitable, as units which quickly hit the cap on their high-growth-rate stats now had an easy method of boosting the low-growth-rate ones.
- Starting with the tenth, if a character does not get at least one stats increased during a level up, the game rerolls (unless a character has hit the cap on everything). Starting with the eleventh game, a character's growth rates will be boosted or dropped if they are behind or ahead of the "average" stats. Like the main example, this helps deal with the very annoying chance that a character gets "RNG Screwed", except this is enough to force a restart on a file in some cases.
- All games after the fifth display inaccurate hit/miss percentages.
- Word of God to the contrary, most players of Puzzle Quest: Challenge of the Warlords believe that the game "nudges" all sort of random stats in its own favor. As many people complain about the computer's habit of chaining together 4/5 gem combos and extra turns, it's even more blatant in Spell Resistance, where an opponent with 2% resistance across the board will block approximately 15% of spells. The player, with the same stats, will be lucky to block one spell in hundreds.
- This trope is often brought up in MMORPGs, where many players believe that item drop rates can be mathematically calculated to determine how many monsters you must kill until you "should" find said item, by assuming that a 1% drop rate means that after you've killed a hundred, something's wrong if you haven't gotten one.note
- City of Heroes actually has a mechanic called the "streakbreaker" that behaves like the second part. For a given base percentage chance to hit, if a player or mob misses a certain number of times in a row, the next hit is guaranteed. For a hit chance below 20%, you have to miss something like a hundred times in a row, but for hit chances above 90%, it only takes one miss to get a guaranteed hit on the next attack. If you were paying REALLY close attention, you could use this to ensure that a key attack doesn't miss.
- Dungeon Fighter Online has a dice roller that is perfectly random for the first instance of every sequence (first upgrade attempt, or random item pickup, or something similar), but then often produces identical results for the next several sets (Failing an identical upgrade five times in a row, the same player getting every single item in a dungeon). It often "corrects" itself and skews the other way until results are even. The hit/miss ratio is the same, either producing a lot of hits or a lot of misses in a row, only rarely looking like the actual statistic.
- The Tetris Guideline has mandated that all Tetris games since around late 2005 have an implementation to make the gambler's fallacy actually happen (and make players complain less of being screwed by the RNG): Instead of rolling a D7 to select a piece, newer Tetris games take a sequence of all seven pieces and deals random permutations of it. Thus, after every seventh piece, all seven have appeared with equal frequency. This also makes every seventh piece completely predictable.
- Prior to that, the Tetris: The Grand Master series also had an algorithm to make the gambler's fallacy come true: The game rolls six times (four in the first TGM) and takes the first result that isn't identical to any of the four most recent pieces dealt. It's still possible for this to "fail" and give you the same pieces over and over again since the game only rolls a fixed number of times; it's just much less likely than with a simple RNG approach.
- The Tetris piece-picking algorithms are many and varied. One, the appropriately named Bastetnote system, picks the worst piece possible for your current situation with an 85% accuracy.
- Prior to that, the Tetris: The Grand Master series also had an algorithm to make the gambler's fallacy come true: The game rolls six times (four in the first TGM) and takes the first result that isn't identical to any of the four most recent pieces dealt. It's still possible for this to "fail" and give you the same pieces over and over again since the game only rolls a fixed number of times; it's just much less likely than with a simple RNG approach.
- Civilization:
- Ask anyone who's played Civilization IV (especially those who play mods like Fall from Heaven) and they will tell you that any combat with less than 80% odds is suicidal and should be avoided at all costs. This sounds crazy, until you reflect that over many battles, an 80% winning chance means losing one battle in five, which (considering the high cost of replacing units) really is a suicidal way to play.
- Alleviated somewhat in V, which is kind enough to give you all of the information BEFORE you attack and provides a rough estimate of where the forces will end up in strength after the round of combat. It was actually criticized heavily for its near-perfect accuracy in prediction! Later patches actually made it a bit more random.
- Not helping matters is that whoever wrote the code for battle predictions fell into this trope themselves. Due to the calculation failing to take several important factors into account, the result varies from "close enough to make a judgment call" to "no connection to what will happen whatsoever." See the Civilization folder under The Computer Is a Cheating Bastard for the details.
- This trope is hugely responsible for the Pokémon entries on The Computer Is a Cheating Bastard, and is the number one thing the game's professional players complain about to similar levels of usage.
- In a more topical instance, players have a random 1/8192 chance of finding an alternately colored Pokémon, similar to albinism and what not. Many players only encounter one or two in several years of playing, others never find one, and some find them with surprising regularity.
- In a similar way, the Pokérus (a "virus" that doubles a Pokémon's stat growth) has a 3/65,536 chance to be on a Pokémon, or 1/3 the probability of finding a "shiny" Pokémon. Many players have never seen the Pokérus, while a few have been lucky enough to get it more than once. Once you have a Pokémon with the Pokérus, though, it's very easy to spread it around the party.
- The first generation did have statistical errors due to bugs, such as attacks that should never miss actually having a 1/256 chance of missing due to the code using "less than" checks instead of "less than or equal to" checks.
- Fortunately, this only applied to the first generation of games. After that, it bypasses the catch calculator entirely.
- Final Fantasy Tactics A2: many people report that attacks that give a 95% success rate fail often. It seems likely that this is the case given the number of complaints (especially since the previous game didn't have these problems - then again, the previous game had an actual flaw in its RNG where success rates tend to be universally higher than the shown numbers suggest) but obviously it's impossible to say for sure.
- XCOM:
- X-COM's accuracy reports during combat aren't exactly blatant lies, but they're not exactly accurate, either. What X-COM does for a hit check is up to two rolls. The first is done against the accuracy check, and if it passes, you automatically get a dead-on shot. The other roll, if the first fails, is the deviation from where you're aiming, which may also end up being nil, resulting in a dead-on shot. So that 75% Accuracy the game reports? More like 77% to hit the target you're aiming at, and up to around 20% to hit someone else, resulting in somewhere around a 86% (on average) chance of someone getting hit by any given shot in a heated battle. Oh, and 100% accuracy reportedly doesn't exist.
- XCOM: Enemy Unknown ditches this in favor of telling player straight how likely he is to hit. However, many players insist that the game cheats in favor of aliens on higher difficulties and Classic mode. This eventually got so bad, that the RNG was taken apart for testing
 by the community... and found to be 100% correct. As it turns out, on the lower difficulties, the computer actually cheat for the player. Thus, once the aid is removed on the higher difficulties, players feel cheated when their "sure" shots no longer hit all the time.
by the community... and found to be 100% correct. As it turns out, on the lower difficulties, the computer actually cheat for the player. Thus, once the aid is removed on the higher difficulties, players feel cheated when their "sure" shots no longer hit all the time.
- Madden NFL:
- The Madden Curse works this way. Generally, the cover is awarded to some athlete who just had a phenomenal season. The next season, the player is often beset by the sorts of bad luck that befall all athletes (injuries, bad games, etc) except they receive more attention. In some cases, it may also be a Self-Fulfilling Prophecy if the player gets a big ego and skimps on workouts, or if other players are more motivated to play hard against him. But mostly it's just that any season of a player is likely to be average (for his or her capabilities) and any season which leads to feature a player in games or magazine stories is likely to be way above average, so it's just a good chance of a "dice roll" showing a lower number, just like the next number after you rolled a six on a normal die is likely to be lower than that. The technical name for this is regression toward the mean
 .
.
- A great example of this would be Brett Lorenzo Favre's appearance on Madden. It appeared that Favre had subverted, nay, broken the Madden curse while playing for the New York Jets. Then the Jets lost four straight games and a bid for the playoffs. "What went wrong," you ask? Brett Favre played the last month of the season with a torn bicep in his throwing arm and no one did anything about it.
- A more direct example are the year-in, year-out complaints that either the stats or the on-field experience are unrealistic, by pointing to the raw numbers. Since Madden is meant to be played with 5-7 minute quarters (rather than 15 as in real-life), this means that gamers are running between 50-70% as many plays as a real NFL contest. Yet many expect to produce as many points or exciting moments, while somehow maintaining realistic results on a per-play basis. This is mathematically impossible. EA chooses the former, heavily slanting the game in favor of the offense.
- The Madden Curse works this way. Generally, the cover is awarded to some athlete who just had a phenomenal season. The next season, the player is often beset by the sorts of bad luck that befall all athletes (injuries, bad games, etc) except they receive more attention. In some cases, it may also be a Self-Fulfilling Prophecy if the player gets a big ego and skimps on workouts, or if other players are more motivated to play hard against him. But mostly it's just that any season of a player is likely to be average (for his or her capabilities) and any season which leads to feature a player in games or magazine stories is likely to be way above average, so it's just a good chance of a "dice roll" showing a lower number, just like the next number after you rolled a six on a normal die is likely to be lower than that. The technical name for this is regression toward the mean
- Crisis Core has the DMW, a slot-machine of various character faces that spins during combat, creating different effects. The only way to level-up is for three "7"s to align on the slots. While this looks like it's leveling based on total randomness, it isn't. The DMW is actually controlled by a complicated mathematical formula that manifests itself as a chance that always just so happens to work out exactly the way natural progression should. In essence, one-in-a-million chances succeed nine times out of ten in this game. Furthermore, while it's not shown anywhere in the game, enemies give experience when killed, increasing the odds of hitting the combination that gives Zack a level up. This means that you're eventually guaranteed to get the 7-7-7 combination that gives you a level up by defeating enough enemies.
- The programmers of Sid Meier's Alpha Centauri fell afoul of this trope when they wrote the code to estimate the battle odds displayed before a combat: they used an obvious-but-wrong method of working out chained probabilities, leading to the game tending to grossly underestimate the actual odds of victory. For example, a strength-8 unit with 30 hitpoints attacking a strength 8 unit with 10 hitpoints would be shown as having a 75% chance of victory; the actual odds of winning are 99.93%. Under the right circumstances, this could result in the game predicting a one-in-a-million chance of winning, when the actual odds are 90%.
- In Achaea, you can flip a coin. Some players argued that the chance was approximately 60/40, rather than the expected 50/50. However, after careful study of the game code, one developer found out that the players were actually right, and corrected the programming error, while also claiming that it wasn't impossible to have the coin fall on edge.
- Discussed and defied in one ending of Stories: Path of Destinies. After discovering that the completed Skyripper could potentially destroy the universe if fired, he discusses the matter further with the sage Calaveras, who narrows it down to a 1 in 128 chance. Reynardo decides this is no big deal; when confronting Zenobia, he even explains the 1 in 128 chance in terms of the Gambler's Fallacy (i.e. that the risk will increase the more he fires the weapon, but the first shot should be perfectly safe), which an exasperated Zenobia points out is not how odds work at all. Needless to say, he fires it, and it destroys the universe.
"One in 128. What are the odds?"
- The video game version of Blood Bowl had the usual complaints about biased RNG and cheating computers. In the sequel, the developers added an after-match screen showing exactly what the dice rolls were for each player. While it is possible to get truly unlucky from time to time, there are enough rolls in a game that the results are usually close to what would be expected from chance. The trick to winning is choosing when to make your rolls so a couple of bad rolls won't lose you the game, while forcing your opponent to make as many rolls as possible so they end up failing something even if they get a lucky streak.
- World End Economica has the protagonist, who is a little full of himself, apply the Gambler's Fallacy to trading on the stock market.
- In Darths & Droids, Pete (R2-D2) likes to "pre-roll the ones out" of his twenty-sided dice. He takes a huge number of dice and rolls them once each, and selects the dice that rolled a one. He rolls those dice again, and selects the dice that rolled one a second time. Since the odds of any given d20 rolling a one three times in a row is 1 in 8,000, another roll of any of these dice has only a 1 in 8,000 chance of rolling a one again, right? ... No.
- Awkward Zombie addresses the matter here
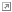 .
"Even after studying statistics, all my knowledge and understanding of it goes out the window when I play Fire Emblem and I get mad at math not doing what I think is best for it."
.
"Even after studying statistics, all my knowledge and understanding of it goes out the window when I play Fire Emblem and I get mad at math not doing what I think is best for it." - Free Fall: Sam Starfall uses statistics in artistic fashion to establish that riding the top of a moving train is safer than climbing a staircase
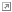 .
.
- Larry Leadhead applies this sort of reasoning to the wargaming tables.
- xkcd likes making fun of this, as seen in the page image. Another example is "Conditional Risk
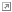 ", in which a character believes that, because "Lightning only kills about 45 Americans a year", it's safe to be out in a thunderstorm, missing that this is because most Americans don't go out in thunderstorms. The caption sardonically claims that the death rate among people who know the stat is one in six.
", in which a character believes that, because "Lightning only kills about 45 Americans a year", it's safe to be out in a thunderstorm, missing that this is because most Americans don't go out in thunderstorms. The caption sardonically claims that the death rate among people who know the stat is one in six.
- Sometimes websites run stories about so-called "winning systems", such as this one
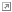 . The most cursory read of the article reveals that the system this guy has "discovered" is merely the martingale, described further up this page.
. The most cursory read of the article reveals that the system this guy has "discovered" is merely the martingale, described further up this page.
- This
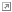 Jalopnik article advocates bringing more diesels to the US market by showing how big of the VW Jetta sales cehunk is diesels. This means next to nothing, since most Jetta buyers buy them for the TDI engine.
Jalopnik article advocates bringing more diesels to the US market by showing how big of the VW Jetta sales cehunk is diesels. This means next to nothing, since most Jetta buyers buy them for the TDI engine.
- A 2016 article claimed that 3% of men and 11% of women were abused as children; it was headlined "14% of adults suffered child abuse". But 3% of half the population plus 11% of the other half adds up to 7% of the total population, not 14%.
- This is parodied in Les Shadoks. The Shadoks' goal for Season 1 is to fail to launch their rocket 999,999 times, as they have calculated that it has a one-in-a-million chance to successfully launch. It doesn't work.
- Family Guy: In the episode "PTV", the PTA claim that "one call equals a billion people", and twenty billion people complained about David Hyde Pierce exposing his testicles on live TV; keep in mind, the world doesn't have anywhere close to that number of people.
- Parodied in The Simpsons, where Disco Stu proclaims that disco sales were up by 400% in 1976, which bodes well if those trends continue. (1976 was twenty years ago at the time.)

